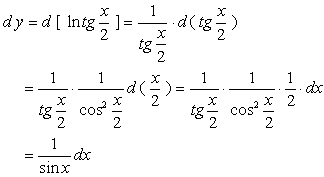§2.7
函数的微分
一、由一个例子引入微分概念
【引例】一块正方形金属薄片受温度变化影响,其边长由![]() 变到
变到![]() ,试给出:
,试给出:
1、此薄片的面积的改变值。
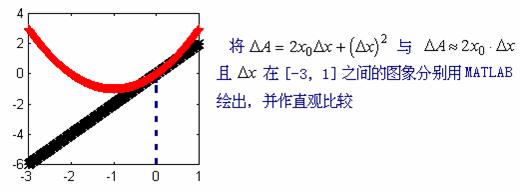
2、用计算机摸拟边长改变量与面积改变量的对应关系
正方形的面积计算公式
![]() ,
,![]() 是边长。
是边长。
当![]() 由
由![]() 变化到
变化到![]() 时, 正方形面积的增量为
时, 正方形面积的增量为
![]()
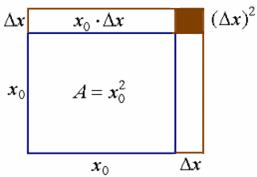
这就是薄片面积的改变量。它由两部分构成:
(1)、![]() 的线性部分
的线性部分![]()
(2)、![]() 的高阶无穷小部分
的高阶无穷小部分![]() (当
(当![]() 时)
时)
直观上,
可以这样解释增量:
![]() 相当小时,
相当小时,![]() 主要取决于第一部分,第二部分对它的影响相对较小,可以忽略不计即:
主要取决于第一部分,第二部分对它的影响相对较小,可以忽略不计即:![]()
微分定义
设函数![]() 在某区间上有定义,
在某区间上有定义,![]() 及
及![]() 在此区间内,若函数增量
在此区间内,若函数增量
![]()
可表示成形式 ![]() (1)
(1)
其中![]() 是不依赖于
是不依赖于![]() 的常数, 而
的常数, 而![]() 是比
是比![]() 更高阶的无穷小。
更高阶的无穷小。
则称函数![]() 在点
在点![]() 是可微的,而
是可微的,而![]() 叫做函数
叫做函数![]() 在点
在点![]() 相应于自变量增量
相应于自变量增量![]() 的微分,记作
的微分,记作![]() 。亦即:
。亦即:![]() 。
。
二、函数可微的充要条件
【定理】函数![]() 在点
在点![]() 可微的充要条件是函数在
可微的充要条件是函数在![]() 处可导。
处可导。
当函数![]() 在
在![]() 处可微时, 其微分为
处可微时, 其微分为 ![]() 。
。
【证明】必要性
因为![]() 在
在![]() 处可微,则(1)式成立
处可微,则(1)式成立
![]()
![]()
![]()
即:![]()
充分性
若函数![]() 在点
在点![]() 可导, 则有
可导, 则有
![]()
![]() 其中
其中 ![]()
![]()
这里,数![]() 是与
是与![]() 无关的常数,而
无关的常数,而![]() 是
是![]() 时的高阶无穷小,故函数
时的高阶无穷小,故函数![]() 在
在![]() 处可微,且微分为
处可微,且微分为 ![]() 。
。
三、常用的结论与概念
1、若![]() ,当
,当![]() 充分小时,有近似公式
充分小时,有近似公式 ![]() 。
。
证明 :![]()

![]()
即:![]() 故:
故: ![]() ( 当
( 当 ![]() 时 )
时 )
2、函数微分
函数![]() 在任意点
在任意点![]() 的微分, 称之为函数的微分,记作
的微分, 称之为函数的微分,记作![]() 或
或![]() 。
。
即:![]()
3、微商
对于函数![]() ,
,
按照微分的记法有 ![]()
按照微分的定义有 ![]()
这表明 ![]() 。
。
因此,![]() 可表示成另一种形式
可表示成另一种形式 ![]()
两边同除![]() 可得
可得 ![]()
亦即:函数微分![]() 与自变量微分
与自变量微分![]() 之商等于函数的导数, 因此导数也叫做微商。
之商等于函数的导数, 因此导数也叫做微商。
过去,我们认为符号![]() 是一个整体记号。现在,可以认为它是函数微分
是一个整体记号。现在,可以认为它是函数微分![]() 与自变量微分
与自变量微分![]() 之商。
之商。
微商的概念与符号是德国数学家莱布尼兹创立的,而导数的概念与符号是由英国数学家牛顿创立的。他们各自沿着不同的途径分别独立地创立了微积分学说,且各自都有独到之处。
牛顿从运动学的观点出发,它给微积分的应用提供了广泛的材料;莱布尼兹从几何学的观点出发,而他所创立的符号系统却十分先进,既表达了概念,又便于运算。象数学软件mathematica的符号演绎系统就采用了莱布尼兹的符号。
当然,牛顿、莱布尼兹二人所创立的微积分决不是我们今天的面貌,它极不严密。被戏称为神秘的微积分学。但它的实际应用成就却令人们欢欣鼓舞。例如,天文学上最伟大的成就之一:海王星的发现,就是数学家利用微积分计算出它的存在性与运动轨迹之后而被天文学家发现的。
马克思也曾对微积分的理论作了研究,并设法使之严谨,这从马克思留下的数学手稿中可以看出这一点。但是,由于没有完整严格的极限理论,使人们对微积分学说一直争论不休。直到数学家哥西与魏尔斯特拉斯的极限理论的诞生,才给微积分学奠定了坚实的理论基础,使它得以蓬蓬勃勃的发展起来。
四、微分的几何意义
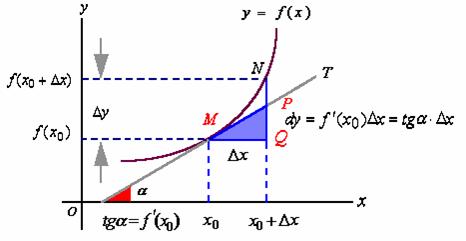
![]() 称之为莱布尼兹微分三角形
称之为莱布尼兹微分三角形
![]() 表示自变量的增量
表示自变量的增量
![]() 表示函数增量
表示函数增量
![]() 表示函数的微分
表示函数的微分
![]() 的意义暂时还不知晓(它代表弧
的意义暂时还不知晓(它代表弧![]() 的微分)
的微分)
五、基本初等函数的微分公式与微分的运算法则
由于函数的微分与导数是等价的,因此,函数的求导法则与求导公式,可以照搬到函数的微分。
这里,我们主要介绍复合函数的微分法则 —— 一阶微分的形式不变。
设![]() ,
,![]() ,则复合函数
,则复合函数![]() 的导数为
的导数为
![]()
它的微分为 ![]()
而 ![]()
故 ![]()
当![]() 为另一个变量的函数,也就是中间变量时,
为另一个变量的函数,也就是中间变量时,![]() 成立,而当
成立,而当![]() 为自变量时,此式显然成立。
为自变量时,此式显然成立。
这一性质被称之为一阶微分的形式不变性。它使求函数微分的过程单一,易于计算机来处理。这也正是莱布尼兹符号体系的优越性。
【例1】 ![]() , 求
, 求 ![]()
解:![]()
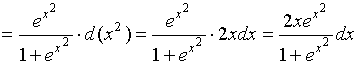
【例2】![]() ,求
,求![]()
解: